Current Divider Calculator
Compute branch currents in parallel resistor circuits using the current divider rule. Supports 2–4 branches, source current or voltage input, and SI/metric units.
Calculation Steps
Circuits · Current divider rule
Current Divider Calculator – overview, formulas & practical examples
This guide explains how the current divider rule works in parallel resistor circuits and how to use the Current Divider Calculator above to split source current or source voltage into branch currents quickly, accurately, and safely.
How to use the Current Divider Calculator step by step
The Current Divider Calculator above is designed to automate the most common current divider tasks you encounter in circuit analysis and basic design: splitting a known source current between parallel resistors, or computing branch currents from a known source voltage. You can choose between 2, 3, or 4 parallel branches, select units, and focus on a particular branch you care about (for example, the current through a sensor or shunt resistor).
At a high level, you will either: (1) provide the total source current and branch resistances, or (2) provide the source voltage and branch resistances. The calculator then applies the current divider rule (or Ohm’s law for each branch) and returns the resulting branch currents, plus helpful quick stats about current share and equivalent resistance.
-
1
Select Calculation Mode: choose By Source Current (IT known) if you know the total current feeding the parallel network, or By Source Voltage (VS known) if you have a voltage source across the branches.
-
2
Set the Number of Parallel Branches (2–4). The calculator automatically shows or hides input rows for Branch 3 and Branch 4 so you only see the fields you need.
-
3
Enter the source value (either IT or VS) with the correct units, then fill in each branch’s resistance R1, R2, R3, and R4 using Ω, kΩ, or MΩ as appropriate. Make sure all resistances are positive and non-zero.
-
4
Choose the Branch to Report if you want the main result card to focus on a particular current (for example, I2). Then click the Calculate button. The Current Divider Calculator will display the selected branch current, the total current or voltage, and a breakdown of how the current splits between branches.
Once you understand this basic workflow, you can use the Current Divider Calculator to quickly explore “what if” scenarios: How does changing one branch resistance affect its current share? What happens to total current if you add a new parallel branch? The calculator handles the math for you, so you can focus on design choices instead of algebra.
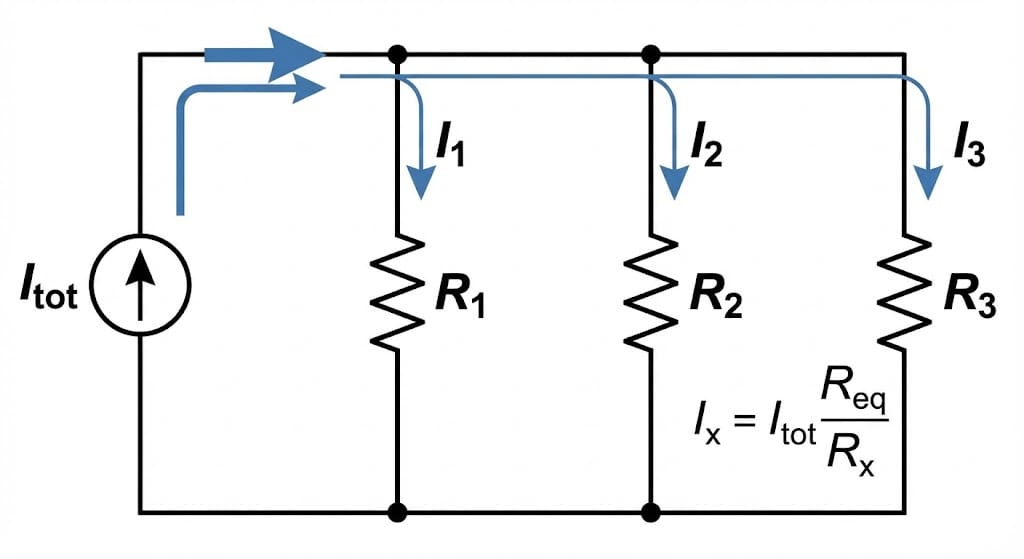
What the current divider rule actually does
A current divider is any parallel network in which a total current IT splits into multiple branch currents I1, I2, I3, … Because all branches share the same voltage (by definition of a parallel connection), the branch with lower resistance carries a larger portion of the total current.
In an ideal parallel resistor network with source current IT:
and each branch current follows Ohm’s law:
Because every branch sees the same voltage \(V\), we can express the ratio of two branch currents in terms of their resistances:
That is the heart of the current divider rule: the branch with the smaller resistance receives the larger current, in inverse proportion to resistance. For two branches, this gives the well-known formulas:
The Current Divider Calculator applies this same logic for up to four branches. Under the hood, it converts all resistances into base units (ohms), computes the equivalent conductance, and then determines how the total current divides among the branches.
Current divider formulas & variables used in the calculator
When you use the Current Divider Calculator, it is helpful to know exactly which variables it is using and how the equations are applied. This section consolidates the core formulas so you can match each input field to the underlying math.
For a general parallel network with \(n\) resistors R1, R2, …, Rn, the branch currents can be written in terms of total current IT as:
The denominator is the total conductance of the network. If the calculator is in By Source Current mode, it uses this expression directly: the IT value you type becomes the total current, and each branch gets a share proportional to its conductance.
The main variables you will see are:
- IT (Source Current) – the total current entering the parallel network, in A or mA.
- VS (Source Voltage) – the voltage across the parallel branches, in V or mV.
- Rk (Branch Resistance) – the resistance of branch \(k\) in Ω, kΩ, or MΩ.
In By Source Voltage mode, the calculator first uses Ohm’s law on each branch:
and then computes the total current as:
It also determines the equivalent resistance of the whole parallel network:
In practice, you do not need to type these equations yourself—the Current Divider Calculator fills its dynamic equation banner with the right form based on your selected mode and number of branches, then evaluates the numeric result using your inputs.
Design tips for sizing parallel branches with a current divider
The current divider rule is not just an academic exercise; it is a powerful design tool when you need to control current in sensing circuits, bias networks, or protective shunts. The key idea is that you can “steer” current into one branch or another by carefully choosing parallel resistances.
Suppose you want a specific branch (say, Branch 1) to carry a target current I1,target from a known total current IT. Rearranging the two-branch divider equation gives you a way to pick R1 and R2:
If you choose one resistor first (for example, a standard value for R2), you can solve for the other to hit your desired current share. The Current Divider Calculator makes this process iterative: change R1 or R2, recalculate, and immediately see how the branch currents shift.
When designing real hardware, keep these practical guidelines in mind:
- Check power dissipation: for each branch, \(P_k = I_k^2 R_k = \dfrac{V^2}{R_k}\). Make sure every resistor’s power rating exceeds its expected dissipation with margin.
- Mind tolerances: resistor tolerances (e.g., ±1%, ±5%) will affect the current split. If the current ratio is critical, use tighter tolerance resistors or verify worst-case conditions.
- Watch total loading: a low equivalent resistance Req increases total current draw from the source. The Current Divider Calculator’s equivalent resistance readout helps you detect excessive loading early.
By combining these design checks with the calculator’s fast iteration, you can quickly converge on a set of resistor values that meet both electrical and thermal constraints.
Troubleshooting & common current divider mistakes
Even with a Current Divider Calculator handling the arithmetic, it is still possible to misinterpret results or build a circuit that behaves differently than expected. This section highlights common pitfalls and how to avoid them.
1. Mixing units incorrectly. If one branch is entered in kΩ and another in Ω, their relative values may be off by a factor of 1,000. Always double-check that each branch resistance uses the intended unit before hitting Calculate.
2. Forgetting the shared voltage assumption. The current divider rule assumes all branches truly are in parallel and share the same voltage. If there are extra series elements or non-linear components (like diodes) in one branch, the simple formulas may no longer apply.
3. Using zero or extremely small resistance values. A branch resistance that is zero or close to zero will dominate the current, potentially exceeding source or component limits. The calculator will warn about invalid or non-physical inputs, but you should also apply engineering judgement.
4. Ignoring temperature and real-world behavior. Resistors heat up and may change value slightly with temperature. Precision current dividers for measurement circuits often use resistors with low temperature coefficients and careful layout to keep them at similar temperatures.
When your simulated or calculated currents do not match lab measurements, start by verifying the exact circuit topology, checking all resistor values with a multimeter, and confirming the source voltage and current limits. The Current Divider Calculator is a great reference for what the ideal divider should do; deviations then help you debug non-ideal effects.
Worked examples with the Current Divider Calculator
To make the formulas concrete, let’s walk through a couple of realistic examples you can reproduce using the Current Divider Calculator. These showcase both calculation modes and highlight how branch resistances shape the current split.
Example 1 – Splitting a 20 mA sensor current between two branches
Imagine you have a 20 mA current source feeding two parallel resistors: R1 = 1 kΩ and R2 = 4.7 kΩ. You want to know how much current flows through each branch, and in particular the current through R1 which is connected to a measurement circuit.
In By Source Current mode, enter IT = 20 mA, R1 = 1 kΩ, and R2 = 4.7 kΩ. The current divider formula for I1 is:
First compute the denominator:
Then the ratio:
and finally the branch current:
The remaining current flows through R2:
Result: The lower-resistance 1 kΩ branch carries around 16.5 mA (about 82% of the total), while the higher-resistance 4.7 kΩ branch carries about 3.5 mA (18%). The Current Divider Calculator will display these currents directly and can also show the equivalent resistance of the pair.
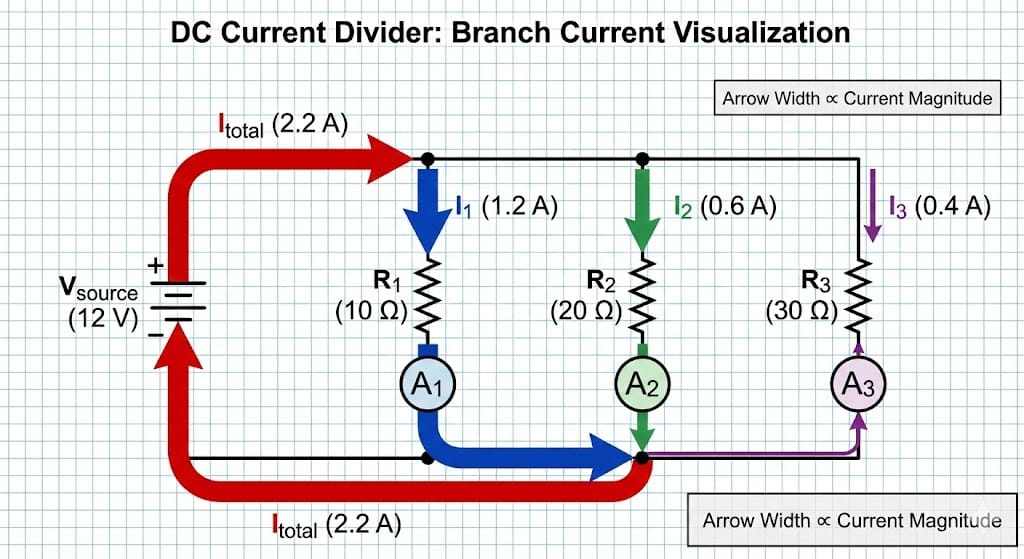
Example 2 – Three-branch divider driven by a 12 V supply
Now consider a 12 V supply feeding three parallel resistors: R1 = 220 Ω, R2 = 330 Ω, and R3 = 1 kΩ. We want to know each branch current and the total current draw from the supply.
Switch the calculator to By Source Voltage mode and enter VS = 12 V with the three resistances listed above. The branch currents follow Ohm’s law:
Numerically:
The total current is the sum of the three:
The equivalent resistance of the network is:
Result: the three branches draw different currents based on their resistances, and together they load the 12 V source with roughly 103 mA. The Current Divider Calculator reports these values instantly and helps you assess whether your supply and resistors are sized appropriately.
Current Divider Calculator – frequently asked questions
What is a current divider in circuit analysis?
A current divider is a parallel circuit in which a total current IT from a source splits into multiple branch currents. Each branch sees the same voltage, but carries a different current depending on its resistance. The current divider rule describes how that total current divides among the branches based on their conductances or resistances.
How do I calculate branch current using the Current Divider Calculator?
Choose the calculation mode based on what you know: use By Source Current if you know IT, or By Source Voltage if you know VS. Then enter the source value, the number of branches, and each branch resistance. After you click Calculate, the tool applies the current divider formulas and displays the current in each branch, highlighting the branch you chose in the “Branch to Report” dropdown.
What is the current divider formula for two parallel resistors?
For two resistors in parallel with total current IT, the branch currents are: \[ I_1 = I_T \cdot \frac{R_2}{R_1 + R_2}, \quad I_2 = I_T \cdot \frac{R_1}{R_1 + R_2}. \] Each branch receives a portion of the total current that is inversely proportional to its resistance. The Current Divider Calculator uses this logic (and its multi-branch generalization) behind the scenes.
When should I use current divider instead of voltage divider?
Use a voltage divider when you have a series chain of resistors and you care about the voltage at one node. Use a current divider when you have a parallel network and care about how an incoming current splits between branches. In many real designs, both concepts appear together: for example, a supply voltage feeding a series resistor that then drives a parallel network, which acts as a current divider.
Can the Current Divider Calculator handle more than two branches?
Yes. The calculator supports 2, 3, or 4 parallel branches. For 3 or 4 branches, it uses the general form of the current divider rule: \[ I_k = I_T \cdot \dfrac{1/R_k}{\sum_j 1/R_j}. \] You can use this to analyze parallel LED strings, sensor networks, or any situation where a single source feeds multiple loads in parallel.
Does the Current Divider Calculator consider power ratings and real-world limits?
The Current Divider Calculator focuses on ideal circuit equations: Ohm’s law, parallel resistance, and the current divider rule. It does not automatically check resistor power ratings or device limits, so you should always verify \(P = I^2 R\) for each branch and confirm that your components and power supply can safely handle the calculated currents. Still, the tool gives you a fast way to estimate branch currents so you can perform those checks with confidence.
