Capacitance Calculator

How to use the Capacitance Calculator step by step

The Capacitance Calculator above lets you quickly solve the ideal capacitor relationship between charge \(Q\), voltage \(V\), and capacitance \(C\), while also giving you stored energy and an RC time constant estimate. You choose which quantity to solve for, enter the other two, and the tool handles the unit conversions and formulas for you.

In its current form, the calculator focuses on a lumped capacitor model (one ideal component). You can:

• Solve for capacitance \(C\) from charge and voltage.
• Solve for charge \(Q\) from capacitance and voltage.
• Solve for voltage \(V\) from capacitance and charge.

The calculator also asks for a reference resistance, which it uses to compute the RC time constant \(\tau = R\,C\). This helps you estimate how fast the capacitor will charge or discharge in a simple RC circuit.

1. 1

   Choose what you want to solve for. In the Solve For dropdown, pick one of: Capacitance (C), Charge (Q), or Voltage (V). For example, if you know the charge and voltage and want the capacitance, choose Capacitance (C).

2. 2

   Enter the known values and units. Fill in the two known fields: Charge (Q) with units like C, mC, µC, or nC, and Voltage (V) in V or kV, or Capacitance (C) in F, mF, µF, nF, or pF. The calculator automatically handles scaling between these units.

3. 3

   Optional: set a reference resistance. Enter a value for the series resistance in Ω, kΩ, or MΩ. This does not change the main result you’re solving for, but it lets the tool compute the RC time constant \(\tau\) and related quick stats.

4. 4

   Read the result and quick stats. The calculator shows the solved value in the Calculated Result row, including the numeric result and units. Below, the quick stats table summarizes the normalized values, stored energy, and RC time constant so you can sanity-check whether the capacitor choice fits your application.

If you scroll to the worked examples, you’ll see step-by-step calculations that match the same fields you’re entering in the Capacitance Calculator.

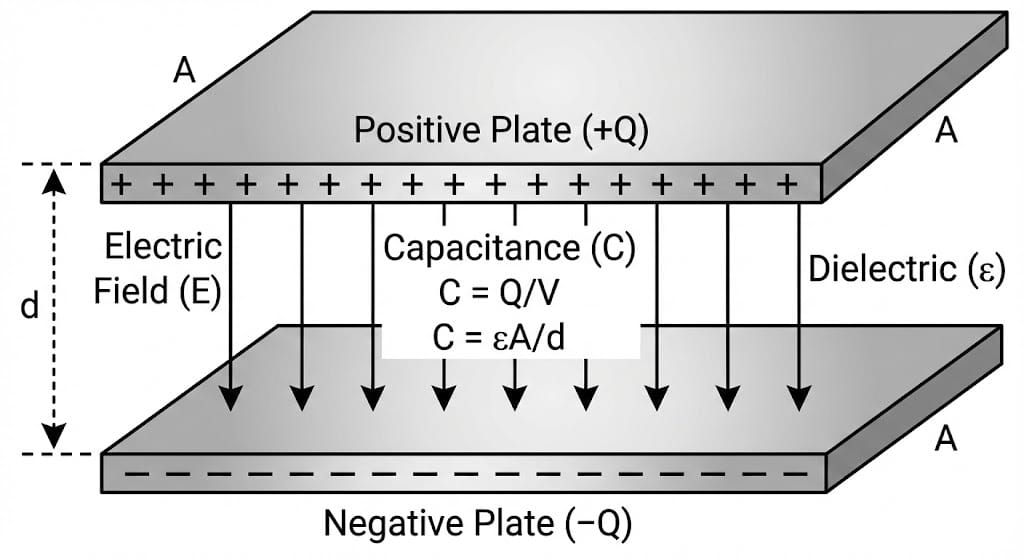
What capacitance is and why it matters in circuits

At its core, capacitance is a measure of how much electric charge a component can store per unit voltage. Mathematically, capacitance is defined as:

where:

• \(C\) is capacitance in farads (F),
• \(Q\) is charge in coulombs (C),
• \(V\) is voltage in volts (V).

One farad is a very large amount of capacitance: it means a capacitor stores 1 coulomb of charge for every 1 volt applied. In real electronic circuits, especially signal-level and digital electronics, you’ll more often see microfarads (\(µF\)), nanofarads (\(nF\)), or picofarads (\(pF\)).

Physically, a capacitor consists of two conductive plates separated by an insulating material (the dielectric). When a voltage is applied, electrons accumulate on one plate and are removed from the other, creating an electric field in the dielectric. The higher the capacitance, the more charge the device can store for a given voltage.

The Capacitance Calculator uses this definition directly: if you pick Solve For: Capacitance (C), it rearranges the equation as \(C = Q/V\). If instead you solve for charge or voltage, it uses the same relationship rearranged:

Capacitance matters because it directly controls how circuits behave dynamically. It affects:

• Filtering and smoothing: larger capacitance smooths out ripple on power supplies.
• Timing and delays: in RC circuits, capacitance works with resistance to set time constants.
• Energy storage: capacitors temporarily store energy for bursts of current or ride-through during brief sags.

When you use the calculator, keep this physical picture in mind: you’re not just crunching numbers; you’re quantifying how “big” the electric charge bucket is for a given voltage.

Key formulas & variables in capacitance calculations

Beyond the basic definition \(C = Q/V\), there are several other important relationships involving capacitance that the Capacitance Calculator helps you work with indirectly. Understanding them will give you more insight into whether your inputs and outputs make sense.

1. Charge–voltage–capacitance relationship

This is often the most convenient form in practical work. If you know the voltage across a capacitor and its capacitance, you can estimate how much charge is stored on its plates. The calculator uses this relationship whenever you solve for \(Q\).

2. Stored energy in a capacitor

A charged capacitor stores energy in its electric field. The energy \(E\) in joules is:

The calculator can display the stored energy as part of its quick stats by taking whatever combination of \(C\) and \(V\) you provide or solve for. This is especially useful when you are sizing capacitors for energy storage or surge suppression applications.

3. Geometric capacitance (parallel-plate approximation)

For a simple parallel-plate capacitor, the capacitance can also be expressed in terms of geometry:

where:

• \(\varepsilon_0\) is the permittivity of free space,
• \(\varepsilon_r\) is the relative permittivity (dielectric constant) of the material between the plates,
• \(A\) is the plate area,
• \(d\) is the separation between plates.

While the current Capacitance Calculator works with the lumped \(Q\)-\(V\)-\(C\) relationship rather than geometric inputs, the result you get from geometry calculations should match the same capacitor behavior plugged into this calculator.

4. Series and parallel combinations

In real circuits, capacitors are often used in series or parallel combinations. The equivalent capacitance is:

Once you compute an equivalent capacitance (for example, of two capacitors in parallel), you can enter that value into the Capacitance Calculator to explore charge, voltage, and energy for the combined network.

• Use \(Q = C\,V\) as the primary relationship for all calculator modes.
• Use the energy equation to verify whether stored energy is realistic for your component size and rating.
• Combine series/parallel capacitors to get an equivalent \(C\) before plugging into the calculator.

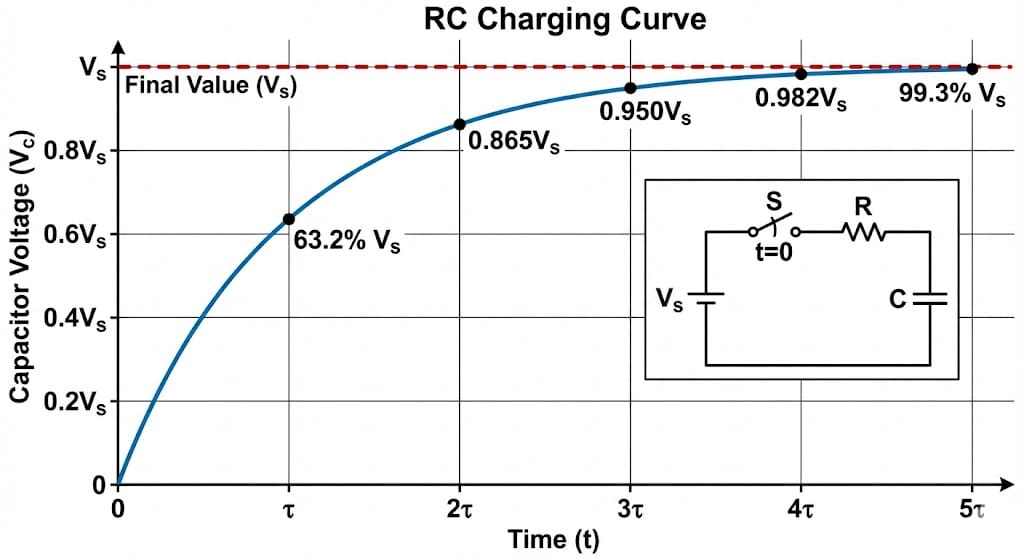
RC time constant and capacitor charge/discharge behavior

Capacitors rarely exist alone; they almost always appear with resistors, wires, and loads. In the simplest case, a capacitor is connected in series with a resistor, forming an RC circuit. The key parameter describing how fast the voltage across the capacitor changes is the time constant \(\tau\):

where \(R\) is resistance in ohms (Ω) and \(C\) is capacitance in farads (F). The Capacitance Calculator asks you for a reference resistance specifically so it can compute this time constant for your chosen \(C\).

For a simple RC charging circuit (capacitor charging from a DC source through a resistor), the voltage across the capacitor as a function of time is:

For discharging (capacitor initially charged, then allowed to discharge through a resistor), the voltage decays exponentially:

Some useful rules of thumb:

• At \(t = \tau\), the capacitor has charged to about 63% of its final value or discharged to about 37% of its initial value.
• At \(t = 5\tau\), the capacitor is effectively “fully” charged or discharged for most practical purposes (>99%).
• Increasing \(C\) or \(R\) increases the time constant and slows down changes.

When you enter a reference resistance and solve for \(C\), the Capacitance Calculator uses these relationships to show an estimated \(\tau\). This is very useful when you are selecting capacitor values for timing circuits (such as RC oscillators, reset delays, or filters) and want to quickly see how changing \(C\) or \(R\) affects response time.

If you’re unsure whether your chosen values make sense, compare the time constant from the calculator with the time scales in your application. For example, a \(\tau\) of 0.1 s might be ideal for a soft-start circuit, but far too slow for high-frequency signal filtering.

Applications and choosing capacitor values in practice

Capacitance shows up everywhere in electrical and electronic systems. Although the Capacitance Calculator focuses on ideal relationships, the results are highly relevant to real applications.

Common applications of capacitors

• Decoupling and bypassing: Capacitors placed near IC power pins smooth out local voltage dips and noise. Typical values range from tens of nF to a few µF, often in ceramic form.
• Bulk energy storage: Larger electrolytic capacitors (tens to hundreds of µF and above) store energy to handle start-up inrush, motor starting, or brief power interruptions.
• Filtering and smoothing: In rectifier circuits, capacitors reduce ripple on DC rails. The required \(C\) depends on load current, acceptable ripple, and line frequency.
• Timing circuits: In combination with resistors, capacitors define delays, pulse widths, and oscillator frequencies using RC time constants.

Using the calculator to size capacitors

Here are typical workflows where the Capacitance Calculator is especially useful:

• Given a desired voltage and charge: Use \(C = Q/V\) to determine the capacitance you need to store that much charge. For example, if you know your circuit needs ~1 mC of charge at 5 V, the calculator tells you that requires \(C = 0.2~\text{mF} = 200~\mu\text{F}\).
• Checking stored energy: After choosing a capacitor value and working voltage, verify that the stored energy is within safe limits for your components and application.
• Matching RC time constants: If you have a target delay or time scale, you can vary \(R\) or \(C\) until the time constant from the calculator matches your requirement.

Voltage rating and component selection

Once you know the required capacitance and operating voltage from the calculator, you still need to choose a physical part. Typical practical guidelines:

• Select a capacitor with a voltage rating comfortably above your maximum operating voltage (often 1.5–2× higher) to allow margin for spikes and tolerances.
• Consider capacitor technology:
  • Ceramic: small, low ESR, good for high-frequency decoupling, but value can vary with voltage and temperature.
  • Electrolytic: large values in small volume, good for bulk storage, but higher ESR and limited lifetime.
  • Film or tantalum: specialized tradeoffs in cost, reliability, and performance.
• Check tolerance, ESR, ripple current rating, and temperature range against your application needs.

Use the Capacitance Calculator for the math, then cross-check with datasheets to make sure your chosen capacitor type and rating are appropriate.

Limitations, tolerances, and safety when using capacitance values

The Capacitance Calculator assumes an ideal capacitor: its capacitance value is exact, it has no losses, and it behaves the same at all frequencies and temperatures. Real components are more complex, so it’s important to understand what the calculator does not model explicitly.

Component tolerances and variation

Real capacitors have tolerances, often ±10%, ±20%, or more, depending on type. A “100 µF” capacitor labeled ±20% might be anywhere from 80 µF to 120 µF. That means the results from the calculator should be treated as nominal values.

• Include tolerance bands when checking timing or energy requirements.
• For critical timing circuits, choose tighter tolerance capacitors or provide adjustment margins in resistance.
• Remember that capacitance can change with temperature, voltage, and aging.

ESR, leakage, and non-ideal effects

Real capacitors exhibit:

• Equivalent series resistance (ESR): causes power dissipation and affects ripple and transient performance.
• Leakage current: small DC path that slowly discharges the capacitor over time.
• Inductance: leads and internal structure create parasitic inductance that matters at high frequencies.

The Capacitance Calculator focuses on the ideal lumped relationships \(Q = C V\), \(E = \tfrac{1}{2} C V^2\), and \(\tau = R C\). If ESR or leakage is critical for your design (such as in switching power supplies or precision timing), you should also evaluate those parameters using component datasheets and more detailed models.

Voltage ratings and safety margins

Perhaps the most important safety rule is never to exceed the capacitor’s voltage rating. Exceeding that limit can cause:

• Gradual degradation and increased leakage.
• Breakdown of the dielectric, leading to shorts.
• In extreme cases, venting or catastrophic failure (especially with electrolytic capacitors).

When you use the calculator to explore charge and energy at a given voltage, always compare the operating voltage to the part’s rating. If the calculator suggests you need ~45 V for your desired energy storage but your capacitor is rated for 35 V, you must choose a higher-rated component or adjust your design.

Finally, remember that the calculator’s outputs represent instantaneous values for a given voltage and capacitance. Real circuits may have transients, noise, and spikes that briefly exceed the nominal values, so build in margin accordingly.

Capacitance Calculator – frequently asked questions

For deeper conceptual explanations or more involved math, you can revisit the sections above or jump back to the how-to-use guide for the Capacitance Calculator.